- 7
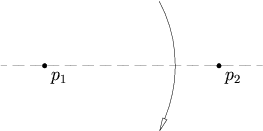
Axiom 1
Given two points p1 and p2, there is a unique fold that passes through both of them.
In parametric form, the equation for the line that passes through the two points is :
Axiom 2
Given two points p1 and p2, there is a unique fold that places p1 onto p2.
This is equivalent to finding the perpendicular bisector of the line segment p1p2. This can be done in four steps:
- Use Axiom 1 to find the line through p1 and p2, given by

- Find the midpoint of pmid of P(s)
- Find the vector vperp perpendicular to P(s)
- The parametric equation of the fold is then:
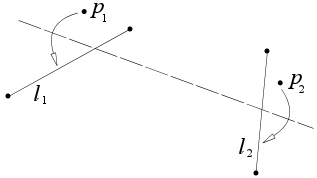
Axiom 3
Given two lines l1 and l2, there is a fold that places l1 onto l2.
This is equivalent to finding a bisector of the angle between l1 and l2. Let p1 and p2 be any two points on l1, and let q1 and q2 be any two points on l2. Also, let u and v be the unit direction vectors of l1 and l2, respectively; that is:
If the two lines are not parallel, their point of intersection is:
where
The direction of one of the bisectors is then:
And the parametric equation of the fold is:
A second bisector also exists, perpendicular to the first and passing through pint. Folding along this second bisector will also achieve the desired result of placing l1 onto l2. It may not be possible to perform one or the other of these folds, depending on the location of the intersection point.
If the two lines are parallel, they have no point of intersection. The fold must be the line midway between l1 and l2 and parallel to them.
Axiom 4
Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.
This is equivalent to finding a perpendicular to l1 that passes through p1. If we find some vector v that is perpendicular to the line l1, then the parametric equation of the fold is:
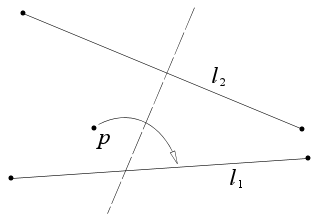
Axiom 5
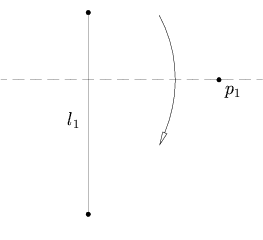
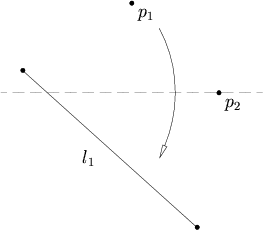
Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.
This axiom is equivalent to finding the intersection of a line with a circle, so it may have 0, 1, or 2 solutions. The line is defined by l1, and the circle has its center at p2, and a radius equal to the distance from p2 to p1. If the line does not intersect the circle, there are no solutions. If the line is tangent to the circle, there is one solution, and if the line intersects the circle in two places, there are two solutions.
If we know two points on the line, (x1, y1) and (x2, y2), then the line can be expressed parametrically as:
Let the circle be defined by its center at p2=(xc, yc), with radius  . Then the circle can be expressed as:
. Then the circle can be expressed as:
In order to determine the points of intersection of the line with the circle, we substitute the x and y components of the equations for the line into the equation for the circle, giving:
Or, simplified:
where:
Then we simply solve the quadratic equation:
If the discriminant b2 − 4ac < 0, there are no solutions. The circle does not intersect or touch the line. If the discriminant is equal to 0, then there is a single solution, where the line is tangent to the circle. And if the discriminant is greater than 0, there are two solutions, representing the two points of intersection. Let us call the solutions d1 and d2, if they exist. We have 0, 1, or 2 line segments:
A fold F1(s) perpendicular to m1 through its midpoint will place p1 on the line at location d1. Similarly, a fold F2(s) perpendicular to m2 through its midpoint will place p1 on the line at location d2. The application of Axiom 2 easily accomplishes this. The parametric equations of the folds are thus:
Axiom 6
Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.
This axiom is equivalent to finding a line simultaneously tangent to two parabolas, and can be considered equivalent to solving a third-degree equation as there are in general three solutions. The two parabolas have foci at p1 and p2, respectively, with directrices defined by l1 and l2, respectively.
This fold is called the Beloch fold after Margharita P. Beloch who in 1936 showed using it that origami can be used to solve general cubic equations.[2]
Axiom 7
Given one point p and two lines l1 and l2, there is a fold that places p onto l1 and is perpendicular to l2.
This axiom was originally discovered by Jacques Justin in 1989 but was overlooked and was rediscovered by Koshiro Hatori in 2002.[3] Robert J. Lang has proven that this list of axioms completes the axioms of origami.
- 4
An axiom is a premise or starting point of reasoning. As classically conceived, an axiom is a premise so evident as to be accepted as true without controversy.[1] The word comes from the Greek ἀξίωμα 'that which is thought worthy or fit,' or 'that which commends itself as evident.'[2][3] As used in modern logic, an axiom is simply a premise or starting point for reasoning,[4] and equivalent to what Aristotle calls a definition.[5] Axioms define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true. Therefore, its truth is taken for granted within the particular domain of analysis, and serves as a starting point for deducing and inferring other (theory and domain dependent) truths. An axiom is defined as a mathematical statement that is accepted as being true without a mathematical proof.[6]
In mathematics, the term axiom is used in two related but distinguishable senses: "logical axioms" and "non-logical axioms". In both senses, an axiom is any mathematical statement that serves as a starting point from which other statements are logically derived. Unlike theorems, axioms (unless redundant) cannot be derived by principles of deduction, nor are they demonstrable by mathematical proofs, simply because they are starting points; there is nothing else from which they logically follow (otherwise they would be classified as theorems).
Logical axioms are usually statements that are taken to be universally true (e.g., (A and B) implies A), while non-logical axioms (e.g., a + b = b + a) are actually defining properties for the domain of a specific mathematical theory (such as arithmetic). When used in the latter sense, "axiom," "postulate", and "assumption" may be used interchangeably. In general, a non-logical axiom is not a self-evident truth, but rather a formal logical expression used in deduction to build a mathematical theory. To axiomatize a system of knowledge is to show that its claims can be derived from a small, well-understood set of sentences (the axioms). There are typically multiple ways to axiomatize a given mathematical domain.
- 3
- 1


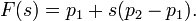











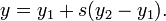



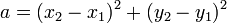

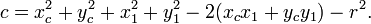
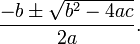


![nbegin{align}nF_1(s) & = p_1 +frac{1}{2}(d_1-p_1)+s(d_1-p_1)^perp [8pt]nF_2(s) & = p_1 +frac{1}{2}(d_2-p_1)+s(d_2-p_1)^perp.nend{align}n](http://upload.wikimedia.org/wikipedia/en/math/6/2/d/62d534f7b4931f9739c597922bf2e9e3.png)